5.3.5. Adjoint Method with Multiple Detector Responses
In this example, we will explore leveraging OpenSn’s adjoint formulation of the linear Boltzmann solver to compute response functions in two Helium-3 detectors within a mockup 2D glovebox.
The following is a complete transport simulation example. Each element of the simulation can be described in the sections below:
5.3.5.1. Prerequisites
Before running this example, make sure that the Python module of OpenSn was installed.
5.3.5.1.1. Converting and Running this Notebook from the Terminal
To run this notebook from the terminal, simply type:
jupyter nbconvert --to python --execute glovebox_adj.ipynb.
To run this notebook in parallel (for example, using 4 processes), simply type:
mpiexec -n 4 jupyter nbconvert --to python --execute glovebox_adj.ipynb.
[ ]:
from mpi4py import MPI
size = MPI.COMM_WORLD.size
rank = MPI.COMM_WORLD.rank
barrier = MPI.COMM_WORLD.barrier
if rank == 0:
print(f"Running the LBS adjoint glovebox example problem with {size} MPI processors.")
5.3.5.1.2. Import Requirements
Import required classes and functions from the Python interface of OpenSn. Make sure that the path to PyOpenSn is appended to Python’s PATH.
[ ]:
import os
import sys
import math
import numpy as np
# assuming that the execute dir is the notebook dir
# this line is not necessary when PyOpenSn is installed using pip
sys.path.append("../../..")
from pyopensn.mesh import FromFileMeshGenerator, PETScGraphPartitioner
from pyopensn.xs import MultiGroupXS
from pyopensn.source import VolumetricSource
from pyopensn.aquad import GLCProductQuadrature2DXY
from pyopensn.solver import DiscreteOrdinatesProblem, SteadyStateSourceSolver
from pyopensn.response import ResponseEvaluator
from pyopensn.math import Vector3, VectorSpatialFunction
from pyopensn.fieldfunc import FieldFunctionInterpolationVolume, \
FieldFunctionInterpolationLine, \
FieldFunctionGridBased
from pyopensn.logvol import RCCLogicalVolume
from pyopensn.context import UseColor, Finalize
5.3.5.2. Geometry
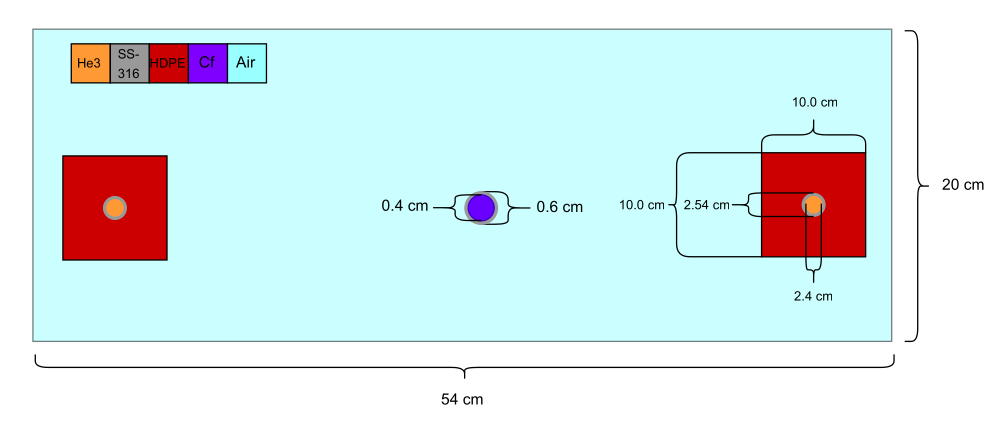
In this example, we define a 2D multigroup, source-driven detector response problem. The neutron source is modeled as a circular region of Cf-252 encased in 0.1 cm of stainless steel (SS-316). Two He-3 detectors are then defined as circular regions of He-3 within SS-316 sleeves, each embedded in a \(10\text{cm}\times 10\text{cm}\) block of high-density polyethylene (HDPE). The geometric layout of the problem is shown below:
5.3.5.3. Mesh
In this section, we import an unstructured mesh generated using the open-source meshing tool Gmsh.
[ ]:
meshgen = FromFileMeshGenerator(
filename="glovebox.msh",
partitioner=PETScGraphPartitioner(type='parmetis'),
)
grid = meshgen.Execute()
grid.SetOrthogonalBoundaries()
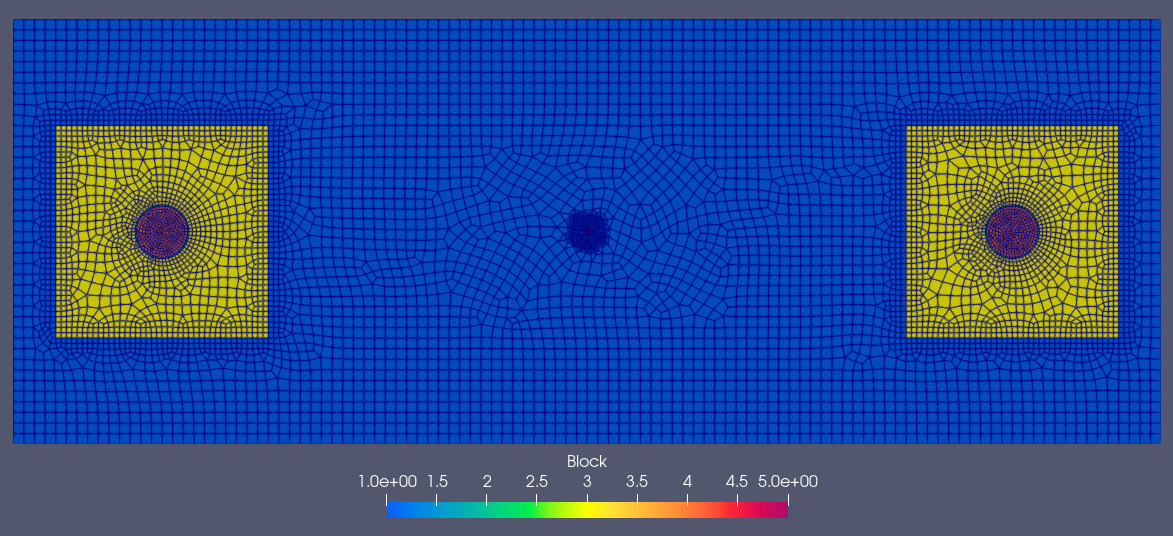


The total cell count for this mesh is 8,214.
5.3.5.3.1. Cross Sections
In this problem we are running a multigroup problem for the absoprtion reaction rate in a He-3 glovebox. This begins with importing our multigroup cross sections. In this case we will be using the WIMS69 group structure for 5 materials:
Air
SS-316
HDPE
He-3
Cf-252
Since we are importing a Gmsh mesh, materials IDs are assigned to the corresponding physcial group ID. Look at glovebox.msh under PhysicalNames.
[ ]:
xs_dir = "WIMS69"
xs_air = MultiGroupXS()
xs_air.LoadFromOpenSn(xs_dir+"/Air.cxs")
xs_steel = MultiGroupXS()
xs_steel.LoadFromOpenSn(xs_dir+"/SS_316.cxs")
xs_hdpe = MultiGroupXS()
xs_hdpe.LoadFromOpenSn(xs_dir+"/HDPE.cxs")
xs_he3 = MultiGroupXS()
xs_he3.LoadFromOpenSn(xs_dir+"/He3.cxs")
xs_cf = MultiGroupXS()
xs_cf.LoadFromOpenSn(xs_dir+"/Cf252.cxs")
xsecs = [{"block_ids": [1], "xs": xs_air},
{"block_ids": [2], "xs": xs_steel},
{"block_ids": [3], "xs": xs_hdpe},
{"block_ids": [4], "xs": xs_he3},
{"block_ids": [5], "xs": xs_cf}]
5.3.5.4. Solver
5.3.5.4.1. Angular Quadrature
Since we are solving a 2D problem we will create Gauss-Legendre Product Quadrature in 2D. In this case we will use 2 polar angles and 128 azimuthal angles. With polar symmetry that leaves us with 128 angles.
[ ]:
pquad = GLCProductQuadrature2DXY(n_polar=2,
n_azimuthal=128,
scattering_order=0)
5.3.5.4.2. Group Structure
Since we are using the WIMS69 group structure, we define a groupset block with 69 energy groups.
[ ]:
num_groups = 69
grpsets = [
{
"groups_from_to": (0, num_groups-1),
"angular_quadrature": pquad,
"inner_linear_method": "petsc_gmres",
"l_abs_tol": 1.0e-9,
"l_max_its": 500,
"gmres_restart_interval": 100,
},
]
5.3.5.4.3. Adjoint Source Definition
To solve the 2D transport problem using the adjoint operator, we first define the adjoint source \(q^{\dagger}\) over the detector volume, assigning a source strength equal to the absorption cross section of the detector, \(\sigma_a^{\text{He3},g}\). By default, adjoint sources are distributed isotropically in angle across the source domain.
To implement this, we create a ResponseFunction. A response function allows us to define the group-wise source strength, which can be used to specify responses in particular energy bins or, in this case, to capture the detector response. To record the response for a specific detector, we set the logical_volume of the adjoint source to the detector of interest.
[ ]:
det1 = [7.0, 10.0, 0.0]
det2 = [47.0, 10.0, 0.0]
dets = [det1, det2]
det_logvols = []
for det in dets:
r_he3 = 1.2
he3 = RCCLogicalVolume(
r=r_he3,
x0=det[0], y0=det[1],
z0=-2.0, vz= 2.0
)
det_logvols.append(he3)
For this initial example, we will be computing the detector response for detector-1, towards the left of the detector.
[ ]:
def ResponseFunction(xyz, mat_id):
response = xs_he3.sigma_a
return response
response_func = VectorSpatialFunction(ResponseFunction)
adj_src = VolumetricSource(logical_volume=det_logvols[0], func=response_func)
5.3.5.4.4. Discrete Ordinates Problem
For the problem block, we provide
mesh : The mesh
num_groups : The number of energy groups
groupsets : The groupsets block
xs_map : Cross section map
volumetric_sources : The volumetric source
boundary_conditions : The boundary conditions
options : Physics solver options
[ ]:
phys = DiscreteOrdinatesProblem(
mesh=grid,
num_groups=num_groups,
groupsets=grpsets,
xs_map=xsecs,
volumetric_sources = [adj_src],
boundary_conditions = [
{"name": "xmin", "type": "vacuum"},
{"name": "xmax", "type": "vacuum"},
{"name": "ymin", "type": "vacuum"},
{"name": "ymax", "type": "vacuum"},
],
options = {"save_angular_flux": True,
"adjoint": True},
)
5.3.5.4.5. Execute
We then create the physics solver, initialize it, and execute it.
[ ]:
ss_solver = SteadyStateSourceSolver(problem=phys)
ss_solver.Initialize()
ss_solver.Execute()
5.3.5.5. Post Processing
5.3.5.5.1. Write Flux Moments
When evaluating response functions via the adjoint formalism its efficiency derives from having access to the adjoint solution \(\phi^{\dagger,g}\). For this, we export the adjoint flux moments to a .h5 file using WriteFluxMoments. The adjoint data is then saved to a location of our choosing.
[ ]:
data_dir = os.getcwd()+"/Data"
os.makedirs(data_dir, exist_ok=True)
phys.WriteFluxMoments(data_dir+"/adjphi_det1_p")
5.3.5.5.2. Detector Response
An adjoint formulation has no meaning without a corresponding forward response. For the volumetric source, we first define the forward source spectrum. In this case, we assign a uniform energy spectrum distributed throughout the source logical volume. Using VolumetricSource, this group-wise source is specified per unit length for material ID 5.
[ ]:
groups = np.flip([1.00000E-11, 5.00000E-09, 1.00000E-08, 1.50000E-08, 2.00000E-08,
2.50000E-08, 3.00000E-08, 3.50000E-08, 4.20000E-08, 5.00000E-08,
5.80000E-08, 6.70000E-08, 8.00000E-08, 1.00000E-07, 1.40000E-07,
1.80000E-07, 2.20000E-07, 2.50000E-07, 2.80000E-07, 3.00000E-07,
3.20000E-07, 3.50000E-07, 4.00000E-07, 5.00000E-07, 6.25000E-07,
7.80000E-07, 8.50000E-07, 9.10000E-07, 9.50000E-07, 9.72000E-07,
9.96000E-07, 1.02000E-06, 1.04500E-06, 1.07100E-06, 1.09700E-06,
1.12300E-06, 1.15000E-06, 1.30000E-06, 1.50000E-06, 2.10000E-06,
2.60000E-06, 3.30000E-06, 4.00000E-06, 9.87700E-06, 1.59680E-05,
2.77000E-05, 4.80520E-05, 7.55014E-05, 1.48729E-04, 3.67263E-04,
9.06899E-04, 1.42510E-03, 2.23945E-03, 3.51910E-03, 5.53000E-03,
9.11800E-03, 1.50300E-02, 2.47800E-02, 4.08500E-02, 6.73400E-02,
1.11000E-01, 1.83000E-01, 3.02500E-01, 5.00000E-01, 8.21000E-01,
1.35300E+00, 2.23100E+00, 3.67900E+00, 6.06550E+00, 1.00000E+01])
group_width = -np.diff(groups)
dE = groups[0] - groups[-1]
dA = np.pi*0.2*0.2
Q = (group_width / dE / dA).tolist()
fwd_src = {'material': [{'block_id': 5, 'strength': Q}]}
With the adjoint data in hand and a forward source defined, we now create a ResponseEvaluator.
We supply two options to the evaluator; the buffers (adjoint data) and the sources.
[ ]:
evaluator = ResponseEvaluator(problem = phys)
evaluator.SetOptions(
buffers = [{
'name': 'detector1',
'file_prefixes': {'flux_moments': data_dir+'/adjphi_det1_p'}
}],
sources = fwd_src
)
For computing the detector response we make use of EvaluateResponse which given a buffer name will compute an inner product of the adjoint flux \(\phi^{\dagger}\) against the forward source \(q\) using the duality principle such that:
At each group the solution \(\phi^g(\vec{r})\) is multiplied by the detector response at that group \(\sigma^{He3,g}_{a}\).
[ ]:
adj_resp = evaluator.EvaluateResponse("detector1")
if rank == 0:
print(f"Total Response Detector 1: {adj_resp:.6e}")
With our field function defined, we can also export the multi-group adjoint flux moments, \(\phi^{\dagger,g}\), to a .vtu file using ExportMultipleToPVTU.
[ ]:
fflist = phys.GetScalarFieldFunctionList(only_scalar_flux=False)
fields = []
for g in range(num_groups):
fields.append(fflist[g][0])
FFGrid = FieldFunctionGridBased
FFGrid.ExportMultipleToPVTU(fields, "AdjFlux/detector1_p")
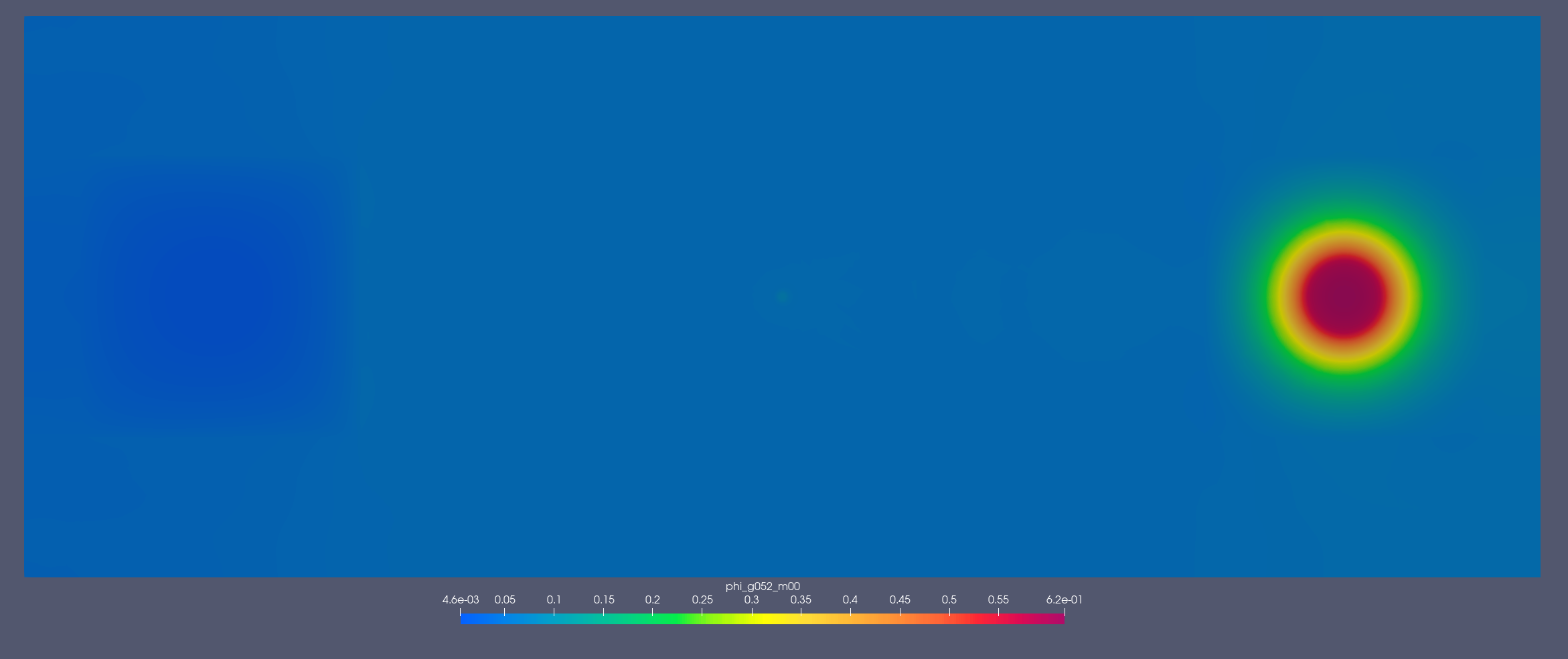
Detector 1:
[1.353, 2.231] MeV
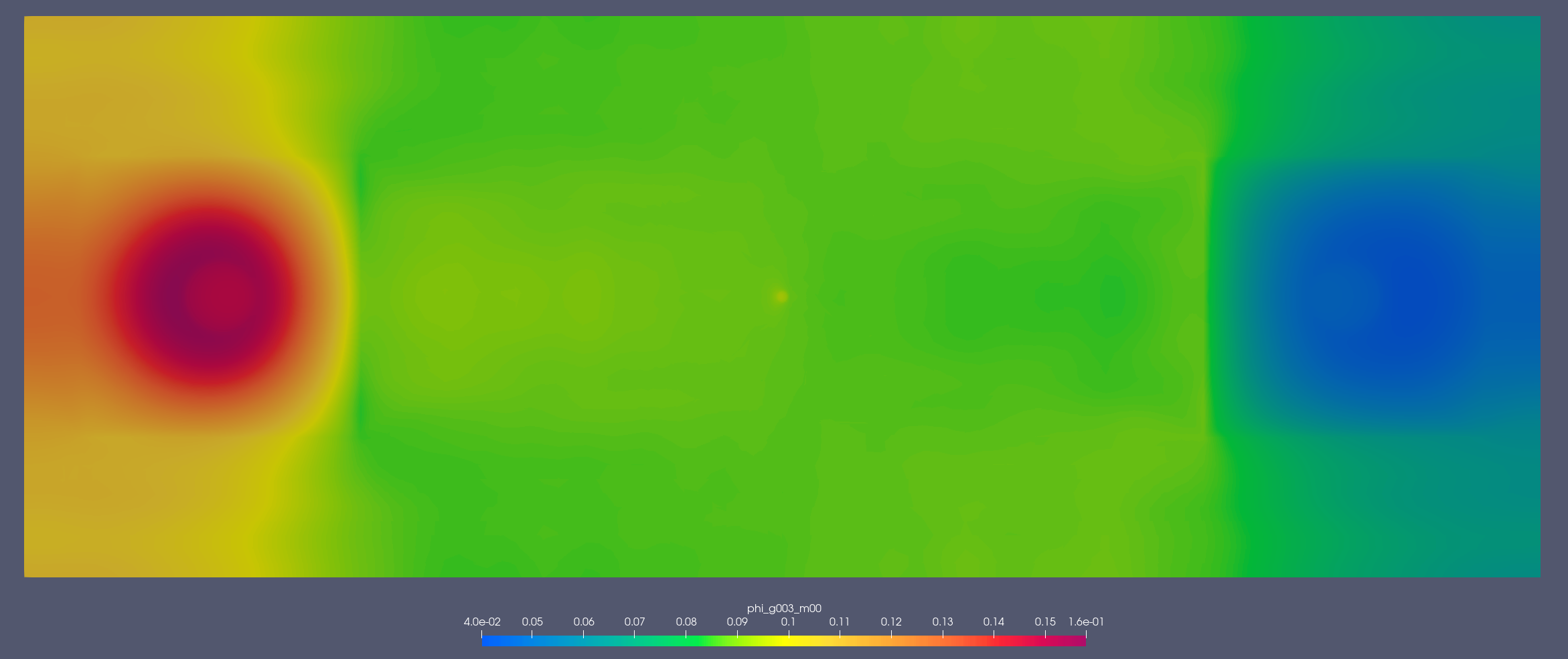
[2.2e-07, 2.5e-07] MeV
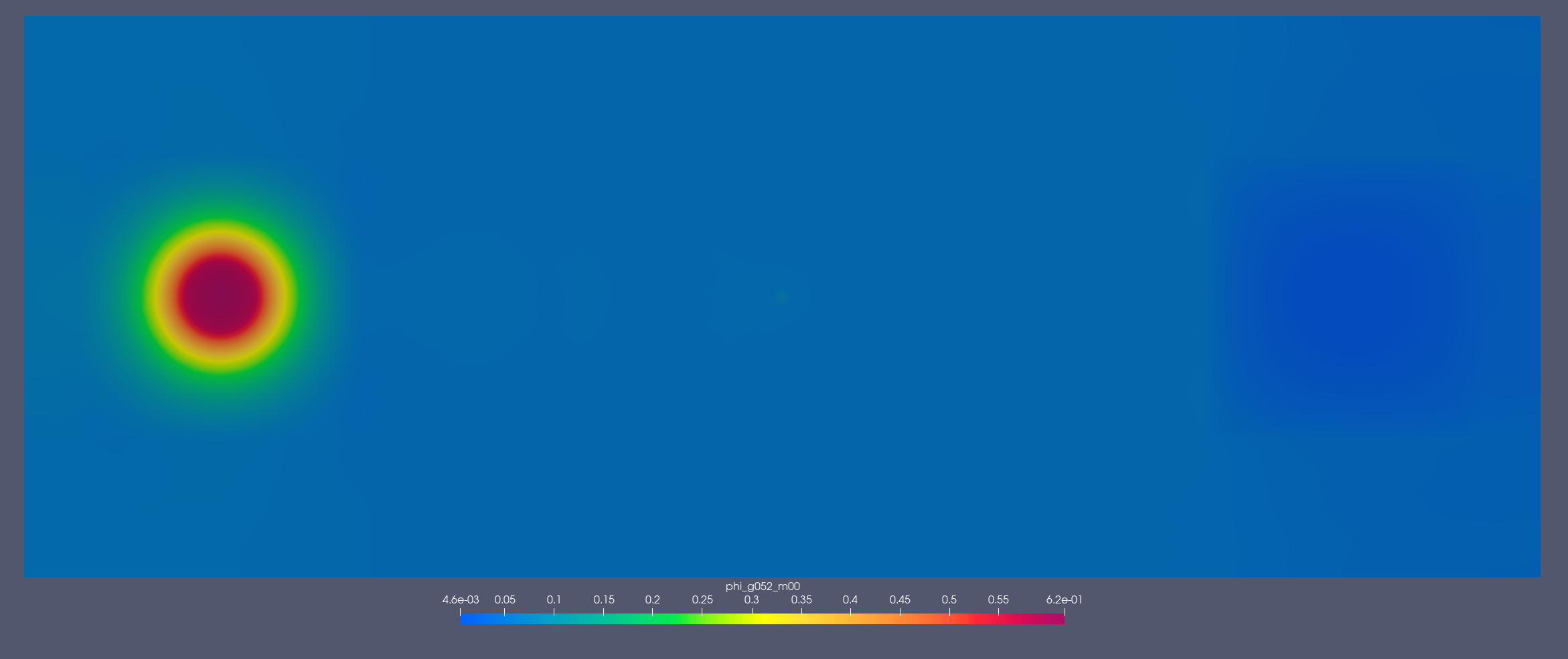
Detector 2:
[1.353, 2.231] MeV
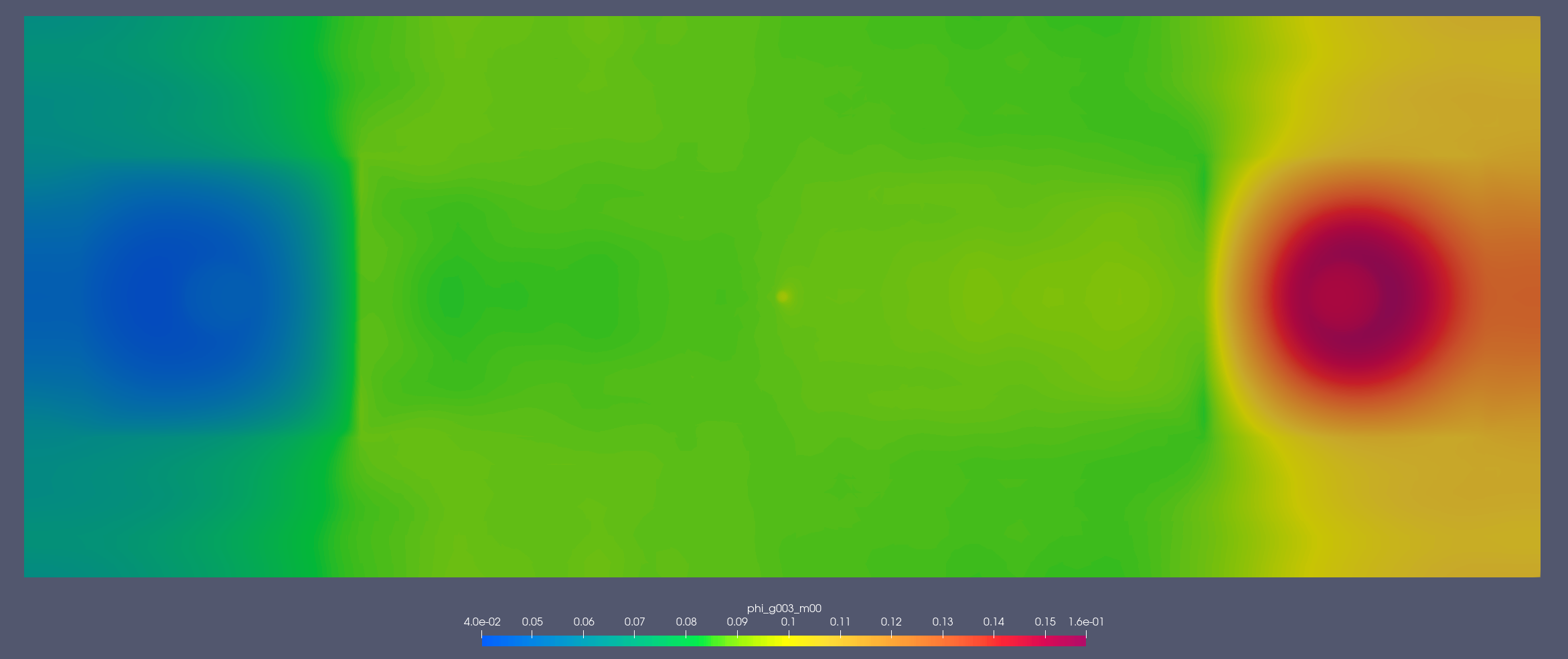
[2.2e-07, 2.5e-07] MeV
5.3.5.6. Finalize (for Jupyter Notebook only)
In Python script mode, PyOpenSn automatically handles environment termination. However, this automatic finalization does not occur when running in a Jupyter notebook, so explicit finalization of the environment at the end of the notebook is required. Do not call the finalization in Python script mode, or in console mode.
Note that PyOpenSn’s finalization must be called before MPI’s finalization.
[ ]:
from IPython import get_ipython
def finalize_env():
Finalize()
MPI.Finalize()
ipython_instance = get_ipython()
if ipython_instance is not None:
ipython_instance.events.register("post_execute", finalize_env)
os.system("rm -rf Data AdjFlux Results")