6. Parallel Sweeps
6.1. Introduction
A parallel sweep algorithm is comprised of the following three components:
Aggregation - The grouping of cells, angles, and groups into tasks. Note that in OpenSn, due to the arbitrary nature of the grid, we don’t aggregate cells.
Partitioning - The division of the mesh among processors.
Scheduling - The execution of available tasks in a specified order by each processor.
Sweep performance is profoundly affected by the choices made for aggregation, partitioning, and scheduling. The interplay of the three components is complex and nuanced, and the reader is referred to the recommended references for more detailed discussions, Mathis et al. [MAA00], Koch et al. [KBA92], Baker and Koch [BK98], Bailey and Falgout [BF09], Pautz [Pau02], Zeyao and Lianxiang [ZL04], Hanebutte and Lewis [HL92], Brown et al. [BCD+99], Brown et al. [BCHW00], Adams et al. [AAH+13], Hawkins et al. [HSA+12], Vermaak et al. [VRAM21]. The content below is only intended to be a very brief introduction to the basic concepts.
6.2. Aggregation
In the previous definitions of the multigroup iterative algorithms, the description of the solution techniques were given on a group-by-group basis. Likewise, the solution of a single-group problem problem was given direction-by-direction. At the level of a given group \(g\), for a given direction \(d\), a full-domain transport sweep is performed where the mesh is swept cell-by-cell, solving for the angular flux \(\psi^g_{d,K}\) in each cell \(K\). A prototypical algorithm following those descriptions is given in Algorithm 1 and shows one potential ordering of the three phase-space loops. Each loop ordering affects code performance in different ways. For example, having the group loop as the outermost loop has the advantage that only one pass through the loop is needed for problems with downscattering only. However, it also leads to a significant number of repeated geometry calculations when sweeping an arbitrary grid. If we swap the group and cell loops so that the group loop is now the innermost loop, we no longer get immediate convergence in problems with downscattering only, but we can re-use geometry information for each group and cell solve. The optimal ordering of loops is problem-dependent, and, while we could introduce separate compute kernels for each ordering, a better solution is to extend our sweep algorithm to support sets of groups and angles.

6.2.1. Group-sets
A group-set is a collection of one or more groups and gives us the flexibility to support different loop orderings without requiring multiple compute kernels. Algorithm 2 extends Algorithm 1 to support group-sets.

If each group is its own group-set, our solution algorithm is similar to Algorithm 1 and is optimal for problems with downscattering only. If all of the groups are contained in a single group-set, the group loop is now the innermost loop, and we can solve all of the groups for each cell concurrently. This greatly increases our flop count and amortizes the cost of querying upwind flux values and other cell-specific quantities.
6.2.2. Angle-sets
Similar to group-sets, angle-sets allow us to group angles together that share similar sweep orderings (they have similar task-directed graphs). With angle-sets, it is possible to solve for multiple angular-flux quantities concurrently on each spatial cell. Angle-sets also allow us to cache common geometric quantities for cell solves and to optimize our sweep-plane data structures for cache efficiency. Algorithm 3 extends our group-set algorithm to include angle-sets.

6.3. Partitioning and Scheduling
Partitioning is the process of dividing the spatial domain among processes. For example, consider the simple 2D mesh shown in Figure 1. This 4x4 mesh has been decomposed among four processors, with each processor being assigned a column of four cells. This columnar decomposition is the type of partitioning produced by the KBA algorithm.
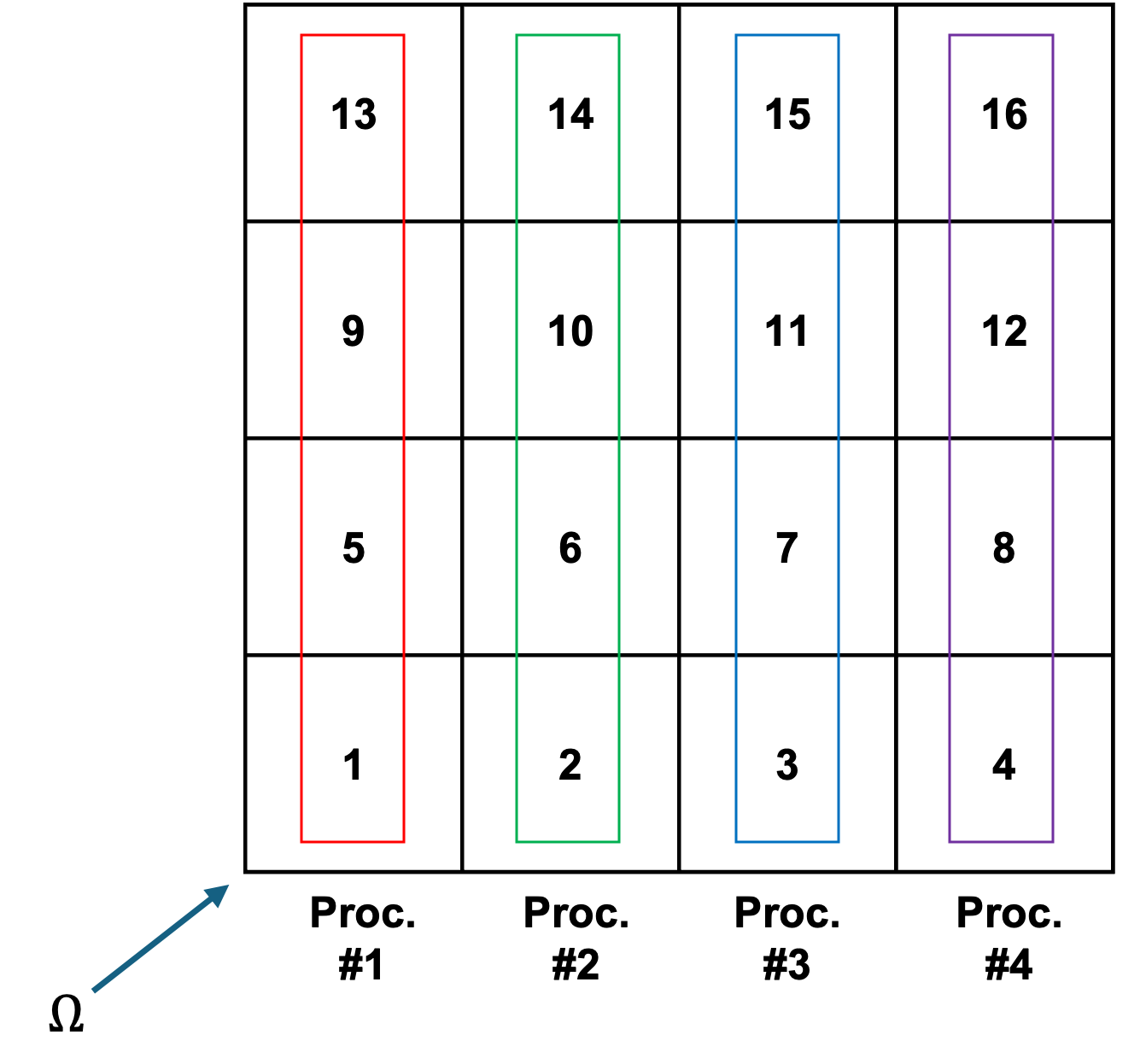
Partitioned, 4x4, XY, Rectangular Mesh
Now, consider the direction \(\vec{\Omega}\) incident on the bottom-left corner of the mesh. The sweep ordering for this quadrature direction is represented by the task-dependency graph shown in Figure 2. As the graph illustrates, a cell on a given level of the graph cannot be solved until its upstream neighbors on the previous level of the graph have been solved. The graph is processed stage by stage, with each processor solving its “ready” cells at each stage and communicating outgoing angular fluxes to its downstream neighbors. As a processor finishes its tasks for one direction in an angle-set, it begins executing its tasks for the next direction until all angles in the angle-set have been processed. Once a processor has finished with one angle-set/group-set combination, it can start solving the next available angle-set/group-set. This pipelining of tasks is important to keep each processor working for as long as possible and to maintain parallel efficiency. In the case where multiple angle-sets can be solved simultaneously, a scheduling algorithm is required to tell the processor the order in which to execute the available tasks.
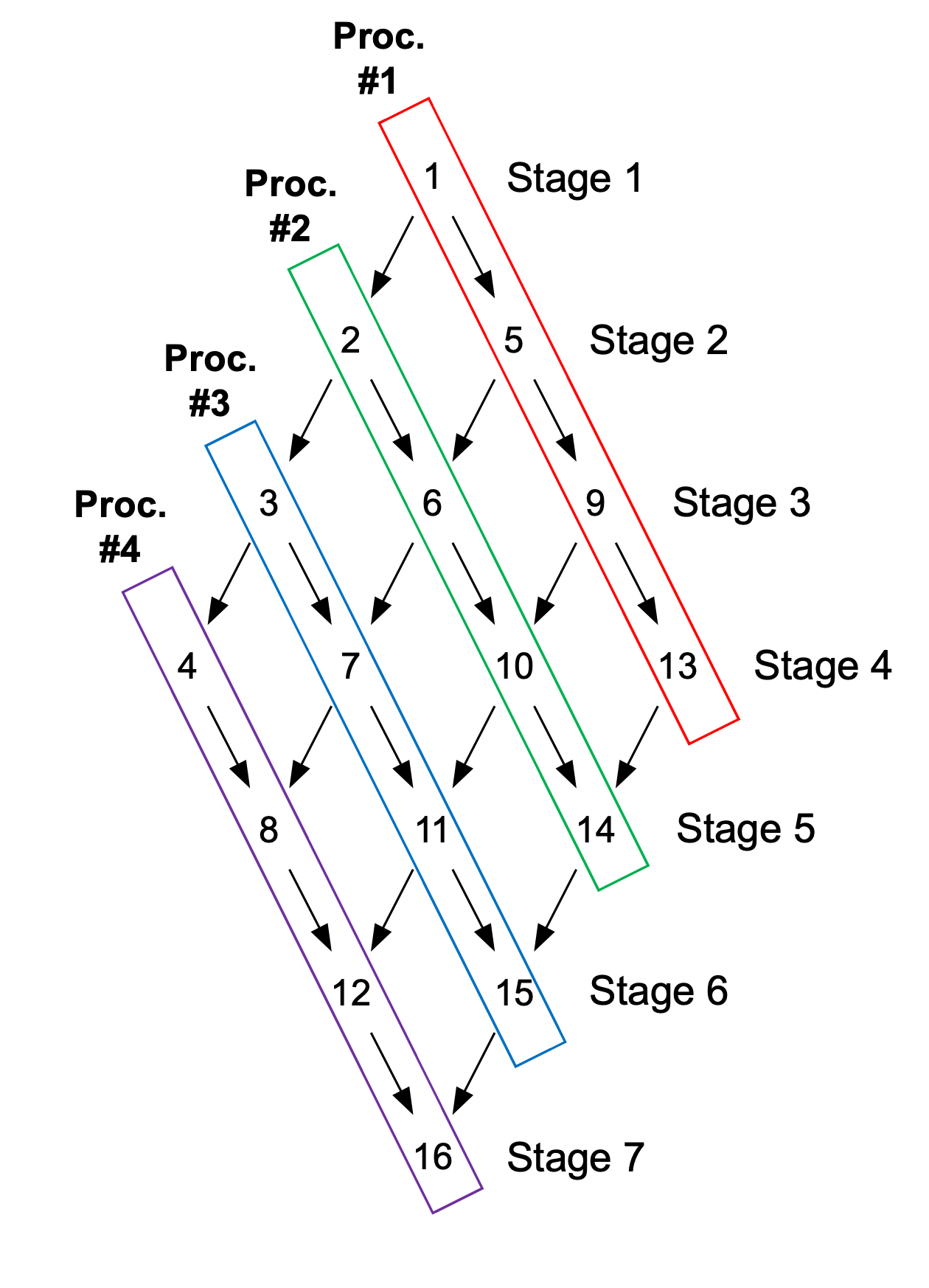
Task Dependency Graph for Direction \(\vec{\Omega}\).
6.4. References
Mark M Mathis, Nancy M Amato, and Marvin L Adams. A general performance model for parallel sweeps on orthogonal grids for particle transport calculations. In Proceedings of the 14th international conference on Supercomputing, 255–263. ACM, 2000.
Kenneth R Koch, Randal S Baker, and Raymond E Alcouffe. Solution of the first-order form of three-dimensional discrete ordinates equations on a massively parallel machine. In Transactions of the American Nuclear Society, volume 65, 198–199. 1992.
Randal S Baker and Kenneth R Koch. An $s_n$ algorithm for the massively parallel cm-200 computer. Nuclear Science and Engineering, 1998.
Teresa S Bailey and Robert D Falgout. Analysis of massively parallel discrete-ordinates transport sweep algorithms with collisions. In International Conference on Mathematics, Computational Methods & Reactor Physics, Saratoga Springs, NY. 2009.
Shawn D Pautz. An algorithm for parallel $s_n$ sweeps on unstructured meshes. Nuclear Science and Engineering, 140(2):111–136, 2002.
Mo Zeyao and Fu Lianxiang. Parallel flux sweep algorithm for neutron transport on unstructured grid. The Journal of Supercomputing, 30(1):5–17, 2004.
UR Hanebutte and EE Lewis. A massively parallel discrete ordinates response matrix method for neutron transport. Nuclear Science and Engineering, 1992.
Peter N Brown, Britton Chang, Milo R Dorr, Ulf R Hanebutte, and Carol S Woodward. Performing three-dimensional neutral particle transport calculations on tera scale computers. In High Performance Computing, volume 99, 11–15. 1999.
PN Brown, B Chang, UR Hanebutte, and CS Woodward. The quest for a high performance boltzmann transport solver. In International conference on applications of high-performance computing in engineering n o, volume 6. 2000.
Michael P Adams, Marvin L Adams, W Daryl Hawkins, Timmie Smith, Lawrence Rauchwerger, Nancy M Amato, Teresa S Bailey, and Robert D Falgout. Provably optimal parallel transport sweeps on regular grids. In Proc. International Conference on Mathematics and Computational Methods Applied to Nuclear Science & Engineering, Idaho. 2013.
William Daryl Hawkins, Timmie Smith, Michael P Adams, Lawrence Rauchwerger, Nancy M Amato, and Marvin L Adams. Efficient massively parallel transport sweeps. In Transactions of the American Nuclear Society, volume 107, 477–481. 2012.
Jan IC Vermaak, Jean C Ragusa, Marvin L Adams, and Jim E Morel. Massively parallel transport sweeps on meshes with cyclic dependencies. Journal of Computational Physics, 425:109892, 2021.